12 junho 2009 12 junho 2009Novas simulações à dinâmica do Sistema Solar, para os próximos 5 mil milhões de anos, obtiveram resultados surpreendentes: Há 1% de hipóteses de a órbita de Mercúrio se desestabilizar nesse período, e como resultado disso, uma ínfima hipótese de Marte, ou mesmo Vénus, chocarem com a Terra. Usando o supercomputador francês JADE, a equipa liderada pelo astrónomo Jacques Laskar, do IMCCE do Observatório de Paris, está a desenvolver a mais completa simulação às órbitas dos planetas do Sistema Solar. Estas simulações incluem factores como a influência gravitacional da Lua sobre a Terra e até efeitos previstos pela teoria da relatividade geral. Numa “letter” publicada na revista nature de 11 de Junho de 2009 , a simulação de Laskar aponta para que, das 2501 órbitas analisadas até há data, 1% delas resultam num aumento da excentricidade de Mercúrio, que provoca distúrbios nas órbitas dos restantes planetas interiores. Em algumas dessas soluções, estas alterações das órbitas levam a encontros muito próximos, ou até colisões entre a Terra e os planetas Marte ou Vénus. Estas não são as únicas colisões possíveis, havendo mesmo um destes resultados que aponta para uma colisão Mercúrio/Marte. Mesmo assim, a acontecerem, nunca ocorreriam nos próximos 3 mil milhões de anos. Mas estes cenários são pouco prováveis (com 99% de hipóteses de não ocorrerem) e dependem de um factor essencial: um grande aumento na excentricidade da órbita de Mercúrio. "Mercúrio é o rastilho, e seria o primeiro planeta a ser desestabilizado por causa da sua pequena massa", disse Laskar. A hipótese mais provável resultante do aumento da excentricidade de Mercúrio seria um "mergulho" deste no Sol. |
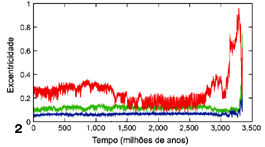
| 1. Representação artística da colisão entre dois planetas (NASA/JPL-Caltech/T. Pyle (SSC/Caltech)) | 2. Gráfico da excentricidade das órbitas de Mercúrio (vermelho), Marte (verde) e Terra (azul) (J. Laskar & M. Gastineau) |